Once similarity intuition has been built with circles, we can start getting into more specific relationships with angles and segments. This post will look at using visual information from central angles and inscribed angles.
Pi Charts
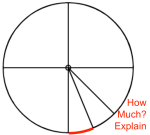
Students sometimes lack intuition for the measure of something. Andrew Stadel has developed this idea into a thorough curriculum on estimation. In my classes we started reasoning through similar exercises. Once we had a decent understanding of circle parts and whole, we moved on to other types of angles.
Non-Central Angles
At this point most students have the common sense that a circle has 360 degrees, and a triangle is half that at 180 degrees. Built with this intuition in mind, we look at a triangle created by inscribed angles.

The next day we get to see the formula that collapses 3 ideas down to 1.
Dynamic Angles in Circles
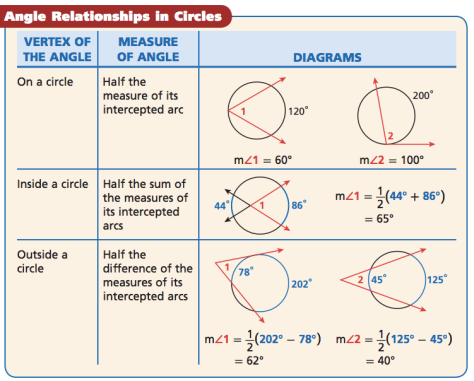
So many of us have tried to organize all the formulas that go with circles. It’s nice when textbooks or other curriculum organizers dom something like:
This is nice, but it still implies that all these relationships are discrete. Instead it would be better to look at them as connected.

I originally thought students would look at this and see how the measures relate. It wasn’t obvious, so I interjected with a simple exercise to the students.
Congruent Overlap
I saw two half sheets (8.25×5.5) of paper on my desk. I held them up and asked the class, “Are these congruent?” The response was something like, “Uh, Duh Mr. Butler.” So I challenged them further, “Would you bet $1,000 on it?”
Now the silent sound of a gambler’s contemplation…
A more valuable decision requires some precision and accuracy. As they were thinking I allowed additional information, “You can’t touch them, but you can ask me to do anything you want.” They took the bait. “Just overlap them, Butler.” Now they’re headed in the right direction. Overlapping layers can reveal congruence or equal measure. Anyone could ask a similar question for an image like these puzzle pieces:

To support the visual information, students need to look at the measures involved and start building the relationships (SMP7 and SMP8). After multiple true versions of the math relationships, we can return to something like the original table.
Students start to see that the table is simply 3 snapshots of this dynamic relationship. Then it is easier to organize the information in their relative schemas. From here we go to paper practice with simple examples and eventually into a more complex question with multiple parts.
Assessment

I took a discrete snapshot from this applet and used it as a paper assessment. Students were solving for complex relationships with multiple layers, and not all with the same process. Common Core math like this requires utilizing big picture relationships while at the same time being able to articulate the specifics within those relationships.
Next time:
This series of dynamic relationships within a circle continues next looking at segments, first with only tangents, and then into various combinations with secants and/or tangents.

Nice post! I think you would love lessons provided on https://schoolyourself.org/ highly interactive and real world examples makes it so easy to learn this concepts.